(本题12分)已知, ∥
∥ ,
, ,试解答下列问题:
,试解答下列问题:
(1)如图所示,则 ___________°,并判断OB与AC平行吗?为什么?
___________°,并判断OB与AC平行吗?为什么?

(2)如图,若点 在线段
在线段 上,且满足
上,且满足 ,并且
,并且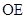 平分
平分 .则
.则 的度数等于_____________°;
的度数等于_____________°;

(3)在第(2)题的条件下,若平行移动 ,如图.
,如图.

①求 :
: 的值;
的值;
②当 时,求
时,求 的度数(直接写出答案,不必写出解答过程).
的度数(直接写出答案,不必写出解答过程).
(本题12分)已知, ∥
∥ ,
, ,试解答下列问题:
,试解答下列问题:
(1)如图所示,则 ___________°,并判断OB与AC平行吗?为什么?
___________°,并判断OB与AC平行吗?为什么?

(2)如图,若点 在线段
在线段 上,且满足
上,且满足 ,并且
,并且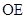 平分
平分 .则
.则 的度数等于_____________°;
的度数等于_____________°;

(3)在第(2)题的条件下,若平行移动 ,如图.
,如图.

①求 :
: 的值;
的值;
②当 时,求
时,求 的度数(直接写出答案,不必写出解答过程).
的度数(直接写出答案,不必写出解答过程).