【2015高考四川，文20】如图，椭圆E：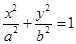
（a>b>0）的离心率是
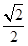，点P（0，1）在短轴CD上，且
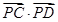＝－1
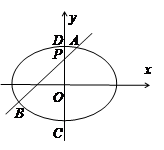
（Ⅰ）求椭圆E的方程；
（Ⅱ）设O为坐标原点，过点P的动直线与椭圆交于A、B两点．是否存在常数λ，使得
为定值？若存在，求λ的值；若不存在，请说明理由．
相关试题
，
，
为正实数，若
，求证：
.
的方程为
，以极点为坐标原点，极轴为
轴的正半轴建立平面直角坐标系，直线
的参数方程为
（
为参数），若直线
的值.
：
，若矩阵
对应的变换将曲线
，求曲线
，
是半径为
的圆
的两条弦，它们相交于
，若
， 
，求
的长.
的前
项和为
，已知
，
.
的等比数列
，其中
，且
，
.
的通项公式；
的不等式
有解，试求推荐套卷
【2015高考四川，文20】如图，椭圆E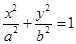：（a>b>0）的离心率是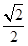，点P（0，1）在短轴CD上，且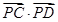＝－1
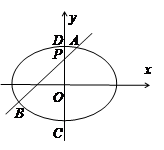
（Ⅰ）求椭圆E的方程；
（Ⅱ）设O为坐标原点，过点P的动直线与椭圆交于A、B两点．是否存在常数λ，使得为定值？若存在，求λ的值；若不存在，请说明理由．
粤公网安备 44130202000953号