为了提高学生写好汉字的积极性,某校组织全校学生参加汉字听写比赛,比赛成绩从高到低只分A、B、C、D四个等级.若随机抽取该校部分学生的比赛成绩进行统计分析,并绘制了如下的统计图表: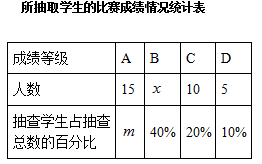
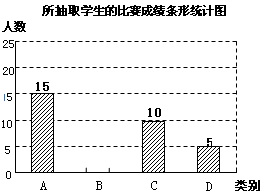
根据图表的信息,回答下列问题:
(1)本次抽查的学生共有 名;
(2)表中 和
和 所表示的数分别为:
所表示的数分别为: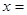 ,
,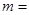 ,并在图中补全条形统计图;
,并在图中补全条形统计图;
(3)若该校共有 名学生,请你估计此次汉字听写比赛有多少名学生的成绩达到B级及B级以上?
名学生,请你估计此次汉字听写比赛有多少名学生的成绩达到B级及B级以上?
相关知识点
推荐套卷
为了提高学生写好汉字的积极性,某校组织全校学生参加汉字听写比赛,比赛成绩从高到低只分A、B、C、D四个等级.若随机抽取该校部分学生的比赛成绩进行统计分析,并绘制了如下的统计图表:

根据图表的信息,回答下列问题:
(1)本次抽查的学生共有 名;
(2)表中 和
和 所表示的数分别为:
所表示的数分别为: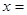 ,
,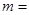 ,并在图中补全条形统计图;
,并在图中补全条形统计图;
(3)若该校共有 名学生,请你估计此次汉字听写比赛有多少名学生的成绩达到B级及B级以上?
名学生,请你估计此次汉字听写比赛有多少名学生的成绩达到B级及B级以上?