如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),翻折矩形OABC,使点A与点C重合,得到折痕DE.设点B的对应点为F,折痕DE所在直线与y轴相交于点G,经过点C、F、D的抛物线为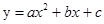 .
.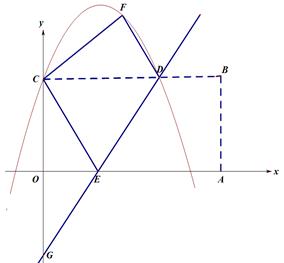
(1)求点D的坐标(用含m的式子表示)
(2)若点G的坐标为(0,-3),求该抛物线的解析式.
(3)在(2)的条件下,设线段CD的中点为M,在线段CD上方的抛物线上是否存在点P,使PM=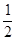 EA?若存在,直接写出P的坐标,若不存在,说明理由.
EA?若存在,直接写出P的坐标,若不存在,说明理由.
相关知识点
推荐套卷

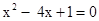 (2)
(2)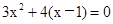
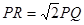 .根据这个结论,解决下面问题:在梯形ABCD中,∠B=45°,AD//BC,AB=5,AD=4,BC=
.根据这个结论,解决下面问题:在梯形ABCD中,∠B=45°,AD//BC,AB=5,AD=4,BC=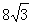 ,P是线段BC上一动点,点P从点B出发,以每秒
,P是线段BC上一动点,点P从点B出发,以每秒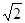 个单位的速度向C点运动.
个单位的速度向C点运动.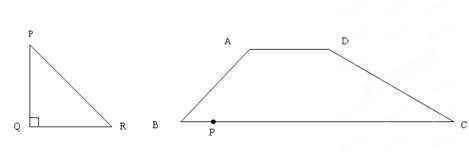
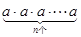 记为
记为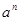 ,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为
,如2·2·2=23=8,此时,3叫做以2为底8的对数,记为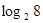 (即
(即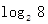 =
=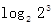 =3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为
=3).②一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为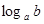 (即
(即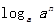 =n),如34=81,则4叫做以3为底81的对数,记为
=n),如34=81,则4叫做以3为底81的对数,记为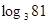 (即
(即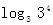 =4).
=4).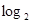 4=" _____________________________" ;
4=" _____________________________" ;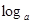 M+
M+
 粤公网安备 44130202000953号
粤公网安备 44130202000953号