(本小题12分)已知 称为x,y的二维平方平均数,
称为x,y的二维平方平均数,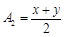 称为x,y 的二维算术平均数,
称为x,y 的二维算术平均数, 称为x,y的二维几何平均数,
称为x,y的二维几何平均数,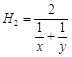 称为x,y的二维调和平均数,其中x,y均为正数。
称为x,y的二维调和平均数,其中x,y均为正数。
(1)试判断 与
与 的大小,并证明你的猜想。
的大小,并证明你的猜想。
(2)令 ,
, ,试判断M与N的大小,并证明你的猜想。
,试判断M与N的大小,并证明你的猜想。
(3)令 ,
, ,
, ,试判断M、N、P三者之间的大小关系,并证明你的猜想。
,试判断M、N、P三者之间的大小关系,并证明你的猜想。
推荐套卷
(本小题12分)已知 称为x,y的二维平方平均数,
称为x,y的二维平方平均数,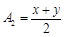 称为x,y 的二维算术平均数,
称为x,y 的二维算术平均数, 称为x,y的二维几何平均数,
称为x,y的二维几何平均数,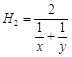 称为x,y的二维调和平均数,其中x,y均为正数。
称为x,y的二维调和平均数,其中x,y均为正数。
(1)试判断 与
与 的大小,并证明你的猜想。
的大小,并证明你的猜想。
(2)令 ,
, ,试判断M与N的大小,并证明你的猜想。
,试判断M与N的大小,并证明你的猜想。
(3)令 ,
, ,
, ,试判断M、N、P三者之间的大小关系,并证明你的猜想。
,试判断M、N、P三者之间的大小关系,并证明你的猜想。