如图,已知二次函数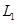 :
: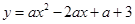 (
(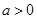 )和二次函数
)和二次函数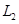 :
: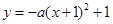 (
(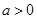 )图象的顶点分别为M,N,与y轴分别交于点E,F.
)图象的顶点分别为M,N,与y轴分别交于点E,F.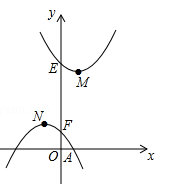
(1)函数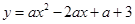 (
(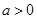 )的最小值为 ,当二次函数
)的最小值为 ,当二次函数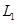 ,
,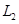 的y值同时随着x的增大而减小时,x的取值范围是 ;
的y值同时随着x的增大而减小时,x的取值范围是 ;
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明);
(3)若二次函数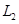 的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程
的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程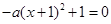 的解.
的解.
相关知识点
推荐套卷
如图,已知二次函数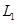 :
: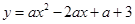 (
(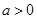 )和二次函数
)和二次函数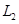 :
: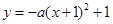 (
(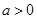 )图象的顶点分别为M,N,与y轴分别交于点E,F.
)图象的顶点分别为M,N,与y轴分别交于点E,F.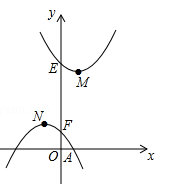
(1)函数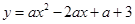 (
(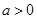 )的最小值为 ,当二次函数
)的最小值为 ,当二次函数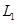 ,
,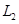 的y值同时随着x的增大而减小时,x的取值范围是 ;
的y值同时随着x的增大而减小时,x的取值范围是 ;
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明);
(3)若二次函数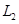 的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程
的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程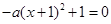 的解.
的解.