已知：直线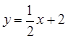
分别与 x轴、y轴交于点A、点B，点P（
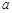，b）在直线AB 上，点P关于
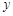轴的对称点P′ 在反比例函数
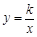图象上．当a=1时，求反比例函数
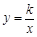的解析式设直线AB与线段P'O的交点为C．当P'C =2CO时，求b的值；
过点A作AD//y轴交反比例函数图象于点D，若AD=
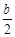，求△P’DO的面积． 
相关试题
与
是同类项，求m、n各是多少
相关知识点
推荐套卷
已知：直线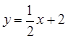分别与 x轴、y轴交于点A、点B，点P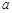（，b）在直线AB 上，点P关于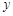轴的对称点P′ 在反比例函数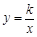图象上．当a=1时，求反比例函数
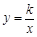的解析式设直线AB与线段P'O的交点为C．当P'C =2CO时，求b的值；
过点A作AD//y轴交反比例函数图象于点D，若AD=
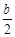，求△P’DO的面积．
粤公网安备 44130202000953号