如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．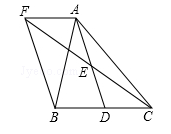
（1）BD与CD有什么数量关系，并说明理由；
（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．
，并从
，
，
中选一个合适的数作为
的值代入求值．
推荐套卷
如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．
（1）BD与CD有什么数量关系，并说明理由；
（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．
粤公网安备 44130202000953号