本题6分)如图,平面直角坐标系中,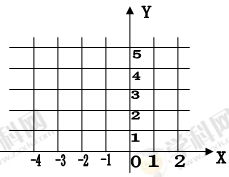
(1)取点A(2,1)、点B(-3,4),则线段AB的长为 ;
(2)若点A的坐标为A(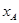 ,
,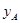 ),点B的坐标为A(
),点B的坐标为A(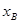 ,
,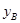 ),则线段AB的长为 (用含
),则线段AB的长为 (用含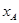 、
、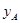 、
、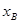 、
、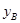 的式子表示);
的式子表示);
(3)△ABC中,已知点A(2,-2)、点B(-3,-1)、点C(-1、-4),请运用(2)中的结论,不画图,用代数方法判断并证明△ABC的形状.
相关知识点
推荐套卷
本题6分)如图,平面直角坐标系中,
(1)取点A(2,1)、点B(-3,4),则线段AB的长为 ;
(2)若点A的坐标为A(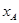 ,
,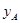 ),点B的坐标为A(
),点B的坐标为A(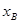 ,
,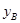 ),则线段AB的长为 (用含
),则线段AB的长为 (用含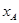 、
、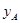 、
、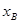 、
、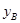 的式子表示);
的式子表示);
(3)△ABC中,已知点A(2,-2)、点B(-3,-1)、点C(-1、-4),请运用(2)中的结论,不画图,用代数方法判断并证明△ABC的形状.