焚烧秸秆是造成雾霾的重要原因,某单位在科研部门的支持下,研发了一套设备,把秸秆转化为一种化工原料.已知该套设备每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)的函数关系为:y= x2-200x+80000,且每处理一吨秸秆得到的化工原料价值为100元.
x2-200x+80000,且每处理一吨秸秆得到的化工原料价值为100元.
(1)设每月获利为S元,求S(元)与x(吨)之间的函数关系式.
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
相关知识点
推荐套卷

 ,其中
,其中 .
.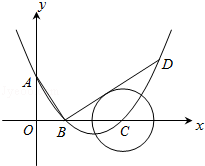
 ,过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点.
,过点C作⊙O的切线交AB的延长线于D点,交AF的延长线于E点.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号