已知一条抛物线和一个椭圆都经过点M(1,2),它们在x轴上具有相同的焦点F1,且两者的对称轴都是坐标轴,抛物线的顶点在坐标原点。
(1)抛物线的方程和椭圆方程;
(2)设椭圆的另一个焦点是F2,经过F2的直线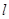 与抛物线交于P,Q两点,且满足
与抛物线交于P,Q两点,且满足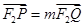 ,求m的取值范围。
,求m的取值范围。
相关知识点
推荐套卷
已知一条抛物线和一个椭圆都经过点M(1,2),它们在x轴上具有相同的焦点F1,且两者的对称轴都是坐标轴,抛物线的顶点在坐标原点。
(1)抛物线的方程和椭圆方程;
(2)设椭圆的另一个焦点是F2,经过F2的直线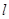 与抛物线交于P,Q两点,且满足
与抛物线交于P,Q两点,且满足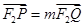 ,求m的取值范围。
,求m的取值范围。