设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
（Ⅰ）求应从这三个协会中分别抽取的运动员人数;
（Ⅱ）将抽取的6名运动员进行编号,编号分别为
A1,A2,A3,A4,A5,A6,从这6名运动员中随机抽取2名参加双打比赛.
   （i）用所给编号列出所有可能的结果;
   （ii）设A为事件"编号为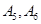
的两名运动员至少有一人被抽到",求事件A发生的概率.
推荐套卷
设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
（Ⅰ）求应从这三个协会中分别抽取的运动员人数;
（Ⅱ）将抽取的6名运动员进行编号,编号分别为
A1,A2,A3,A4,A5,A6,从这6名运动员中随机抽取2名参加双打比赛.
   （i）用所给编号列出所有可能的结果;
   （ii）设A为事件"编号为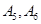的两名运动员至少有一人被抽到",求事件A发生的概率.
粤公网安备 44130202000953号