(本小题满分13分)已知无穷数列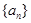 的各项均为正整数,
的各项均为正整数,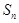 为数列
为数列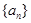 的前
的前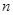 项和.
项和.
(Ⅰ)若数列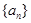 是等差数列,且对任意正整数
是等差数列,且对任意正整数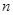 都有
都有 成立,求数列
成立,求数列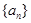 的通项公式;
的通项公式;
(Ⅱ)对任意正整数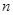 ,从集合
,从集合 中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与
中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与 一起恰好是1至
一起恰好是1至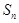 全体正整数组成的集合.
全体正整数组成的集合.
(ⅰ)求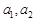 的值;
的值;
(ⅱ)求数列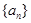 的通项公式.
的通项公式.
相关知识点
推荐套卷
(本小题满分13分)已知无穷数列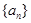 的各项均为正整数,
的各项均为正整数,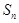 为数列
为数列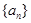 的前
的前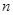 项和.
项和.
(Ⅰ)若数列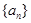 是等差数列,且对任意正整数
是等差数列,且对任意正整数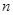 都有
都有 成立,求数列
成立,求数列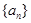 的通项公式;
的通项公式;
(Ⅱ)对任意正整数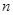 ,从集合
,从集合 中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与
中不重复地任取若干个数,这些数之间经过加减运算后所得数的绝对值为互不相同的正整数,且这些正整数与 一起恰好是1至
一起恰好是1至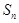 全体正整数组成的集合.
全体正整数组成的集合.
(ⅰ)求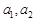 的值;
的值;
(ⅱ)求数列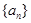 的通项公式.
的通项公式.