某校从参加高二年级学业水平测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．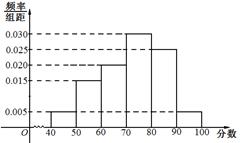
（I）估计这次测试数学成绩的平均分；
（II）假设在[90，100]段的学生的数学成绩都不相同，且都超过94分．若将频率视为概率，现用简单随机抽样的方法，从95，96，97，98，99，100这6个数中任意抽取2个数，有放回地抽取了3次，记这3次抽取中，恰好是两个学生的数学成绩的次数为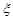
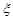，求的分布列及数学期望
．
的前
项和为
，
；
，
时，解不等式
；
，解关于
的不等式
满足：
， 
，
，前
项和为
的数列
满足：
满足
，求数列
的前n项和
，解不等式
；
的不等式
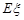相关知识点
推荐套卷
某校从参加高二年级学业水平测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．
（I）估计这次测试数学成绩的平均分；
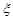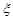（II）假设在[90，100]段的学生的数学成绩都不相同，且都超过94分．若将频率视为概率，现用简单随机抽样的方法，从95，96，97，98，99，100这6个数中任意抽取2个数，有放回地抽取了3次，记这3次抽取中，恰好是两个学生的数学成绩的次数为，求的分布列及数学期望．
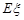粤公网安备 44130202000953号