在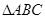 中,
中, 现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。
现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。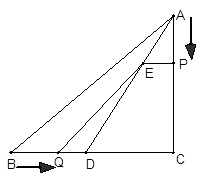
(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在BD(不包括点B、D)上移动时,设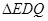 的面积为
的面积为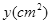 ,求
,求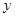 与月份
与月份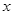 的函数关系式,并写出自变量
的函数关系式,并写出自变量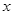 的取值范围;
的取值范围;
(3)当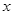 为何值时,
为何值时,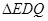 为直角三角形。
为直角三角形。
相关知识点
推荐套卷
在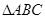 中,
中,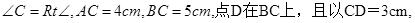 现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。
现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动。过点P作PE∥BC交AD于点E,连结EQ。设动点运动时间为x秒。
(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在BD(不包括点B、D)上移动时,设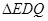 的面积为
的面积为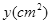 ,求
,求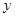 与月份
与月份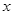 的函数关系式,并写出自变量
的函数关系式,并写出自变量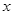 的取值范围;
的取值范围;
(3)当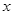 为何值时,
为何值时,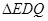 为直角三角形。
为直角三角形。