已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O 上运动(不与点B重合),连接CD,且CD=OA.
(1)当OC=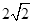 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线;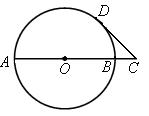
(2)当OC>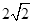 时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
①当D为CE中点时,求△ACE的周长;
②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE·ED的值;若不存在,请说明理由。
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O 上运动(不与点B重合),连接CD,且CD=OA.
(1)当OC=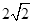 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线;
(2)当OC>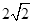 时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
①当D为CE中点时,求△ACE的周长;
②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE·ED的值;若不存在,请说明理由。