清明期间，某校师生组成200个小组参加“保护环境，美化家园”植树活动．综合实际情况，校方要求每小组植树量为2至5棵，活动结束后，校方随机抽查了其中50个小组，根据他们的植树量绘制出如图所示的两幅不完整统计图．请根据图中提供的信息，解答下面的问题：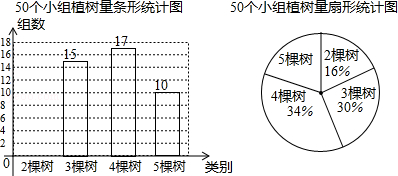
（1）请把条形统计图补充完整，并算出扇形统计图中，植树量为“5棵树”的圆心角是 °．
（2）请你帮学校估算此次活动共种多少棵树．
如图，已知在△ABC中，AB=AC，BC比AB大3，
，点G是△ABC的重心，AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
（1）求AG的长；
（2）当∠APQ=90º时，直线PG与边BC相交于点M.求
的值；
（3）当点Q在边AC上时，设BP=
，AQ=
，求关于的函数解析式，并写出它的定义域.[
如图，已知在平面直角坐标系xOy中，抛物线
与x轴交于点A、B（点A在点B右侧），与y轴交于点C(0，-3)，且OA=2OC．
（1）求这条抛物线的表达式及顶点M的坐标；
（2）求
的值；
（3）如果点D在这条抛物线的对称轴上，且∠CAD=45º，求点D的坐标.
已知：如图，在正方形ABCD中，点E是边AD的中点，联结BE，过点A作
,分别交BE、CD于点H、F，联结BF．
（1）求证：BE=BF；
（2）联结BD，交AF于点O，联结OE．求证：
甲、乙两车都从A地前往B地，如图分别表示甲、乙两车离A地的距离S（千米）与时间t（分钟）的函数关系.已知甲车出发10分钟后乙车才出发，甲车中途因故停止行驶一段时间后按原速继续驶向B地，最终甲、乙两车同时到达B地，根据图中提供的信息解答下列问题：
（1）甲、乙两车行驶时的速度分别为多少？
（2）乙车出发多少分钟后第一次与甲车相遇？
（3）甲车中途因故障停止行驶的时间为多少分钟？
粤公网安备 44130202000953号