如图，在直角坐标系中，A点在x轴上，AB∥y轴，C点在y轴上，CB∥x轴，点B的坐标为（8，10），点D在BC上，将△ABD沿直线AD翻折，使得点B刚好落在y轴的点E处．
（1）求△CDE的面积；
（2）求经过A、D、O三点的抛物线的解析式；
（3）点M是（2）中抛物线上的动点,点N是其对称轴上的动点,问是否存在这样的点M和点N,使得以A、E、M、N为顶点的四边形是平行四边形？若存在,请直接写出点M和点N的坐标;若不存在,请说明理由．
相关试题
阅读下面材料：点A、B在数轴上分别表示数a，b，A、B两点之间的距离表示为
。
当A、B两点中有一点在原点时，不妨设点A在原点，如图(1)，
当A、B两点都不在原点时，
①如图(2)，点A、B都在原点的右边，
；
②如图(3)，点A、B都在原点的左边，
；
③如图(4)，点A、B都在原点的两边，
；
综上，数轴上A、B两点之间的距离
。
回答下列问题：(1)数轴上表示2和5的两点之间的距离是▲．
(2)数轴上表示－1和－5的两点之间的距离是▲；
(3)数轴上表示1和－4的两点之间的距离是▲；
(4)数轴上表示x和－1的两点A之和B之间的距离是▲，如果
＝2，那么x的值是▲．
某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元。厂方在开展促销活动期间，向客户提供两种优惠方案：
①买一套西装送一条领带；
②西装和领带都按定价的90%付款。
现某客户要到该服装厂购买西装20套，领带x条（x>20）。(1)若该客户按方案①购买，需付款▲元（用含x的代数式表示）；
若该客户按方案②购买，需付款▲元（用含x的代数式表示）°(2)若x＝30，通过计算说明此时按哪种方案购买较为合算？
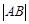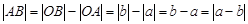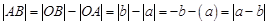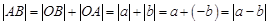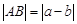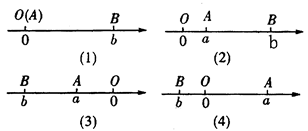
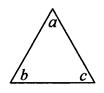
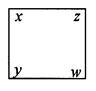若“三角” 表示运算a－b＋c，若“方框”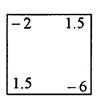 
>
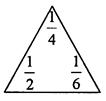
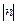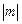，请将下列各数描在数轴上，并用“<”号连接：m，n，相关知识点
推荐套卷
粤公网安备 44130202000953号