（年广西南宁10分）在平面直角坐标系中, 抛物线
与直线
交于A, B两点，点A在点B的左侧．
（1）如图1，当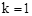
时，直接写出A，B两点的坐标；
（2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
（3）如图2，抛物线
与x轴交于C，D两点（点C在点D的左侧）．在直线上是否存在唯一一点Q，使得∠OQC=90°？若存在，请求出此时k的值；若不存在，请说明理由．
（年广西南宁10分）在平面直角坐标系中, 抛物线与直线交于A, B两点，点A在点B的左侧．
（1）如图1，当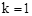时，直接写出A，B两点的坐标；
（2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
（3）如图2，抛物线与x轴交于C，D两点（点C在点D的左侧）．在直线上是否存在唯一一点Q，使得∠OQC=90°？若存在，请求出此时k的值；若不存在，请说明理由．
（m为整数且m>1）
、
、
、
，________，__________；
，求
的值.
粤公网安备 44130202000953号