(本题14分)如图,⊙M与x轴交于A.B两点,其坐标分别为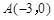 、
、 ,直径CD⊥x轴于N,抛物线
,直径CD⊥x轴于N,抛物线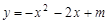 经过A.B.D三点,
经过A.B.D三点,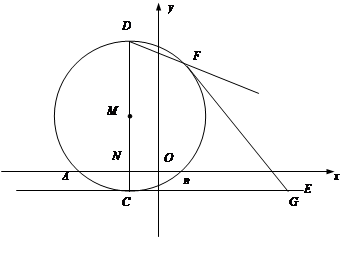
(1)求m的值及点D的坐标.
(2)若直线CE切⊙M于点C,G在直线CE上,已知点G的横坐标为3. 求G的纵坐标
(3)对于(2)中的G,是否存在过点G的直线,使它与(1)中抛物线只有一个交点,请说明理由.
(4)对于(2)中的G直线FG切⊙M于点F,求直线DF的解析式.
相关知识点
推荐套卷
(本题14分)如图,⊙M与x轴交于A.B两点,其坐标分别为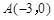 、
、 ,直径CD⊥x轴于N,抛物线
,直径CD⊥x轴于N,抛物线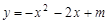 经过A.B.D三点,
经过A.B.D三点,
(1)求m的值及点D的坐标.
(2)若直线CE切⊙M于点C,G在直线CE上,已知点G的横坐标为3. 求G的纵坐标
(3)对于(2)中的G,是否存在过点G的直线,使它与(1)中抛物线只有一个交点,请说明理由.
(4)对于(2)中的G直线FG切⊙M于点F,求直线DF的解析式.