已知数列{
}中,
,且
对任意正整数都成立,数列{}的前n项和为
（1）若
,且
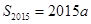,求a；
（2）是否存在实数k,使数列{}是公比不为1的等比数列,且任意相邻三项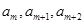
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由；
（3）若
．
相关试题
有且只有一个解，求实数
的值。
，
，且
，
的取值范围。(本题8分)
的解集.(本题6分)
，(
，比较
与
的大小；
时，有
，求实数
的取值范围.
元，获得总利润
元.推荐套卷
已知数列{}中,,且对任意正整数都成立,数列{}的前n项和为
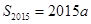（1）若,且,求a；
（2）是否存在实数k,使数列{}是公比不为1的等比数列,且任意相邻三项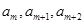按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由；
（3）若．
粤公网安备 44130202000953号