(本小题12分)已知函数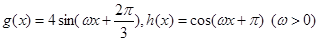 .
.
(Ⅰ)当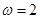 时,把
时,把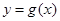 的图像向右平移
的图像向右平移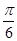 个单位得到函数
个单位得到函数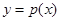 的图像,求函数
的图像,求函数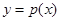 的图像的对称中心坐标;
的图像的对称中心坐标;
(Ⅱ)设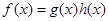 ,若
,若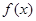 的图象与直线
的图象与直线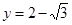 的相邻两个交点之间的距离为π,求
的相邻两个交点之间的距离为π,求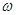 的值,并求函数
的值,并求函数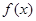 的单调递增区间.
的单调递增区间.
相关知识点
推荐套卷
(本小题12分)已知函数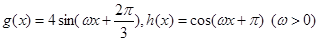 .
.
(Ⅰ)当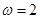 时,把
时,把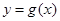 的图像向右平移
的图像向右平移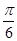 个单位得到函数
个单位得到函数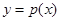 的图像,求函数
的图像,求函数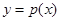 的图像的对称中心坐标;
的图像的对称中心坐标;
(Ⅱ)设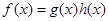 ,若
,若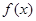 的图象与直线
的图象与直线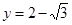 的相邻两个交点之间的距离为π,求
的相邻两个交点之间的距离为π,求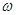 的值,并求函数
的值,并求函数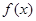 的单调递增区间.
的单调递增区间.