山东省实验中学为了活跃师生的课外文化生活，在2015年3月中旬举办了一次知识竞赛，经过层层筛选，最后五名同学进入了总决赛．在进行笔答题知识竞赛中，最后一个大题是选做题，要求参加竞赛的五名选手从2道题中选做一道进行解答，假设这5位选手选做每一题的可能性均为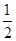
，求
（Ⅰ）其中甲乙2位选手选做同一道题的概率．
（Ⅱ）设这5位选手中选做第1题的人数为x，求x的分布列及数学期望．
0，
.
值； (2)求
的值.
.
在闭区间
上的最大值是1？若存在，求出对应的a值？若不存在，试说明理由．
，x∈R(其中A＞0，ω＞0,
)的周期为π，且图象上一个最低点为M
.
时，求f(x)的最大值．
，
.
值； (2)求
的值.相关知识点
推荐套卷
山东省实验中学为了活跃师生的课外文化生活，在2015年3月中旬举办了一次知识竞赛，经过层层筛选，最后五名同学进入了总决赛．在进行笔答题知识竞赛中，最后一个大题是选做题，要求参加竞赛的五名选手从2道题中选做一道进行解答，假设这5位选手选做每一题的可能性均为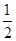，求
（Ⅰ）其中甲乙2位选手选做同一道题的概率．
（Ⅱ）设这5位选手中选做第1题的人数为x，求x的分布列及数学期望．
粤公网安备 44130202000953号