(本小题满分15分)某飞机失联,经卫星侦查,其最后出现在小岛 附近.现派出四艘搜救船
附近.现派出四艘搜救船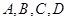 ,为方便联络,船
,为方便联络,船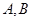 始终在以小岛
始终在以小岛 为圆心,100海里为半径的圆上,船
为圆心,100海里为半径的圆上,船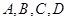 构成正方形编队展开搜索,小岛
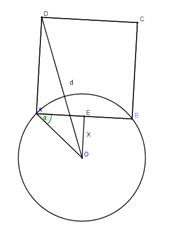
构成正方形编队展开搜索,小岛 在正方形编队外(如图).设小岛
在正方形编队外(如图).设小岛 到
到 的距离为
的距离为 ,
,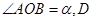 船到小岛
船到小岛 的距离为
的距离为 .
.
(1)请分别求 关于
关于 的函数关系式
的函数关系式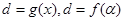 ;并分别写出定义域;
;并分别写出定义域;
(2)当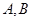 两艘船之间的距离是多少时搜救范围最大(即
两艘船之间的距离是多少时搜救范围最大(即 最大).
最大).
推荐套卷
(本小题满分15分)某飞机失联,经卫星侦查,其最后出现在小岛 附近.现派出四艘搜救船
附近.现派出四艘搜救船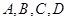 ,为方便联络,船
,为方便联络,船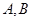 始终在以小岛
始终在以小岛 为圆心,100海里为半径的圆上,船
为圆心,100海里为半径的圆上,船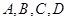 构成正方形编队展开搜索,小岛
构成正方形编队展开搜索,小岛 在正方形编队外(如图).设小岛
在正方形编队外(如图).设小岛 到
到 的距离为
的距离为 ,
,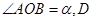 船到小岛
船到小岛 的距离为
的距离为 .
.
(1)请分别求 关于
关于 的函数关系式
的函数关系式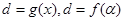 ;并分别写出定义域;
;并分别写出定义域;
(2)当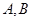 两艘船之间的距离是多少时搜救范围最大(即
两艘船之间的距离是多少时搜救范围最大(即 最大).
最大).