（本小题满分13分）某巡逻艇在A处发现北偏东45
相距9海里的C处有一艘走私船，正沿南偏东75的方向以10海里/小时的速度逃窜.
（Ⅰ）若巡逻艇计划在正东方向进行拦截，问巡逻艇应行驶到什么位置进行设卡？
（Ⅱ）若巡逻艇立即以14海里/小时的速度沿着直线方向追击，问经多少时间后巡逻艇恰追赶上该走私船？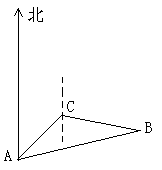
相关试题
中，
，
． 
的值；
，求
（ω＞0）
）上是增函数，求ω最大值
的最小正周期、最大值、最小值
最小正周期为π，最大值为3，且
≠0），求f (x)的的解析式。相关知识点
推荐套卷
（本小题满分13分）某巡逻艇在A处发现北偏东45相距9海里的C处有一艘走私船，正沿南偏东75的方向以10海里/小时的速度逃窜.
（Ⅰ）若巡逻艇计划在正东方向进行拦截，问巡逻艇应行驶到什么位置进行设卡？
（Ⅱ）若巡逻艇立即以14海里/小时的速度沿着直线方向追击，问经多少时间后巡逻艇恰追赶上该走私船？
粤公网安备 44130202000953号