（本小题满分12分）某校在一次对学生在课外活动中喜欢跑步和喜欢打球的学生的抽样调查
中，随机抽取了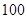
名同学，相关数据如下表所示：
| |
喜欢跑步 |
喜欢打球 |
总计 |
| 男生 |
 |
 |
 |
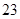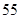| 女生 |
 |
 |
 |
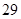| 总计 |
 |
 |
|
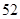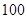（1）由表中数据直观分析，喜欢打球的学生是否与性别有关？
（2）用分层抽样的方法在喜欢打球的学生中随机抽取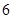
名，求男学生应该抽取几名？
（3）在上述抽取的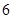名学生中任取
名，求恰有
名女学生的概率．
相关试题
的右焦点为
，设左顶点为A，上顶点为B且
，如图．
的方程；
，过
的直线
交椭圆于
两点，试确定
的取值范围．已知函数
在
处取得极小值．
（1）若函数
的极小值是
，求；
（2）若函数的极小值不小于
，问：是否存在实数
，使得函数在
上单调递减？若存在，求出的范围；若不存在，说明理由．
如图，在多面体ABCDEF中，底面ABCD是梯形，且AD=DC=CB=
AB．直角梯形ACEF中，
，
是锐角，且平面ACEF⊥平面ABCD．
（1）求证：
；
（2）若直线DE与平面ACEF所成的角的正切值是
，试求的余弦值．
求：
；
．
.推荐套卷
粤公网安备 44130202000953号