已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.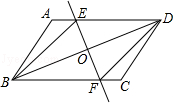
(1)求证:OE=OF.
(2)当∠DOE等于 度时,四边形BFDE为菱形。(直接填写答案即可)
相关知识点
推荐套卷
已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:OE=OF.
(2)当∠DOE等于 度时,四边形BFDE为菱形。(直接填写答案即可)