本题共有3个小题,第(1)小题满分4分,第(2)小题满分7分,第(3)小题满分7分.
各项均为正数的数列 的前
的前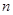 项和为
项和为 ,且对任意正整数
,且对任意正整数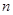 ,都有
,都有 .
.
(1)求数列 的通项公式;
的通项公式;
(2)如果等比数列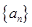 共有
共有 项,其首项与公比均为
项,其首项与公比均为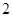 ,在数列
,在数列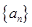 的每相邻两项
的每相邻两项 与
与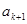 之间插入
之间插入 个
个 后,得到一个新的数列
后,得到一个新的数列 .求数列
.求数列 中所有项的和;
中所有项的和;
(3)如果存在 ,使不等式
,使不等式 成立,求实数
成立,求实数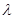 的范围.
的范围.
推荐套卷
本题共有3个小题,第(1)小题满分4分,第(2)小题满分7分,第(3)小题满分7分.
各项均为正数的数列 的前
的前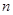 项和为
项和为 ,且对任意正整数
,且对任意正整数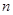 ,都有
,都有 .
.
(1)求数列 的通项公式;
的通项公式;
(2)如果等比数列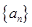 共有
共有 项,其首项与公比均为
项,其首项与公比均为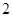 ,在数列
,在数列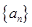 的每相邻两项
的每相邻两项 与
与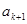 之间插入
之间插入 个
个 后,得到一个新的数列
后,得到一个新的数列 .求数列
.求数列 中所有项的和;
中所有项的和;
(3)如果存在 ,使不等式
,使不等式 成立,求实数
成立,求实数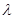 的范围.
的范围.