某区体育局组织篮球技能大赛,每名选手都要进行运球、传球、投篮三项比赛,每名选手在各项比赛中获得合格与不合格的机会相等,且互不影响．现有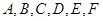
六名选手参加比赛,体育局根据比赛成绩对前
名选手进行表彰奖励．
（1）求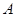
至少获得一个合格的概率；
（2）求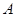与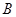
只有一个受到表彰奖励的概率．
是
的直径，直线
与
，
平分
．
；
， 
，求
等于弦
，过
作
的切线
，取
，
交
，
交
，则
和
的度数分别是多少?
中,
．求证:
．
与
相交于点
、
，且
点在
，分别与
、
，过点
分别与
、
，
交
于
点．
； （2）
．
推荐套卷
某区体育局组织篮球技能大赛,每名选手都要进行运球、传球、投篮三项比赛,每名选手在各项比赛中获得合格与不合格的机会相等,且互不影响．现有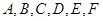六名选手参加比赛,体育局根据比赛成绩对前名选手进行表彰奖励．
（1）求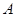至少获得一个合格的概率；
（2）求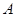与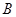只有一个受到表彰奖励的概率．
粤公网安备 44130202000953号