（本小题满分12分）某校高三文科（1）班学生参加“大联考”，其数学成绩（已折合成百分制）的频率分布直方图如图所示，其中成绩分布区间为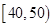
，
，
，
，
，
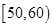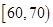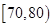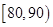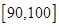，现已知成绩落在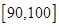的有
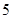人．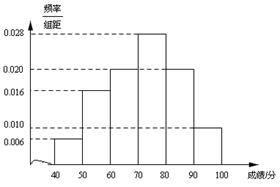
（1）求该校高三文科（1）班参加“大联考”的总人数；
（2）根据频率分布直方图，估计该班此次数学成绩的平均分（可用中值代替各组数据的平均值）；
（3）现要从成绩在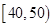和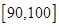的学生中共选
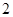人参加某项座谈会，求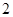人来自于同一分数段的概
率．
相关试题
中，
是
的中点，
.
平面
； 
的平面角的余弦值.
满足：
,且
是
,
的等差中项.
,
,求
.
中，
、
、
分别为角
所对的边，且
.
的大小；
, 且
, 求
的值．
(
R,且
)的部分图象如图所示．
的值；
在
内有两个不同的解,求实数m的取值范围．
为锐角
的三个内角，向量
与
共线．
的大小和求角
的取值范围；
的单调性并求其值域．推荐套卷
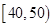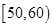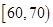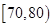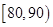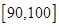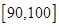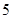（本小题满分12分）某校高三文科（1）班学生参加“大联考”，其数学成绩（已折合成百分制）的频率分布直方图如图所示，其中成绩分布区间为，，，，，，现已知成绩落在的有人．
（1）求该校高三文科（1）班参加“大联考”的总人数；
（2）根据频率分布直方图，估计该班此次数学成绩的平均分（可用中值代替各组数据的平均值）；
（3）现要从成绩在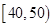和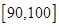的学生中共选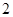人参加某项座谈会，求人来自于同一分数段的概
率．
粤公网安备 44130202000953号