（本小题满分12分）已知直线
所经过的定点
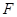恰好是椭圆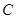
的一个焦点，且椭圆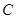上的点到点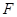的最大距离为8.
（1）求椭圆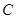的标准方程；
（2）设直线AB过点
且与椭圆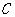
相交于点A、B，
是否为定值，若是求出这个定值，若不是说明理由。
相关试题
的前
项和为
，且满足
，
，数列
的前
，若
对一切
恒成立，求
的最小值．
为偶函数．且
的值；
在
上的单调性，并证明你的结论；
在
上有解，求
的取值范围？
的最值； （2）是否存在
的值使
？
与
共线，其中A是△ABC的内角。
的大小； （2）若
，求
的最大值。
.
在
为减函数；
的不等式
.推荐套卷
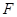（本小题满分12分）已知直线所经过的定点恰好是椭圆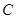的一个焦点，且椭圆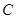上的点到点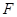的最大距离为8.
（1）求椭圆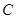的标准方程；
（2）设直线AB过点且与椭圆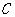相交于点A、B，是否为定值，若是求出这个定值，若不是说明理由。
粤公网安备 44130202000953号