(本小题满分14分)
有限数列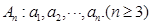 同时满足下列两个条件:
同时满足下列两个条件:
①对于任意的 (
( ),
),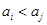 ;
;
②对于任意的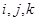 (
( ),
),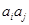 ,
, ,
,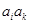 三个数中至少有一个数是数列
三个数中至少有一个数是数列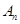 中的项.[来
中的项.[来
(1)若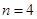 ,且
,且 ,
, ,
,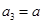 ,
, ,求
,求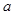 的值;
的值;
(2)证明: 不可能是数列
不可能是数列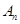 中的项;
中的项;
(3)求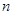 的最大值.
的最大值.
推荐套卷
(本小题满分14分)
有限数列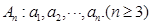 同时满足下列两个条件:
同时满足下列两个条件:
①对于任意的 (
( ),
),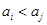 ;
;
②对于任意的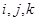 (
( ),
),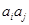 ,
, ,
,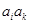 三个数中至少有一个数是数列
三个数中至少有一个数是数列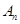 中的项.[来
中的项.[来
(1)若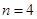 ,且
,且 ,
, ,
,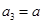 ,
, ,求
,求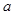 的值;
的值;
(2)证明: 不可能是数列
不可能是数列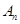 中的项;
中的项;
(3)求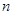 的最大值.
的最大值.