（本小题满分14分）如图，在四棱锥P-ABCD中，四边形ABCD是直角梯形，AB⊥AD，AB∥CD，PC⊥底面ABCD，PC=AB=2AD=2CD=2，E是PB的中点．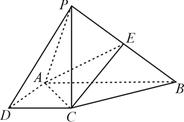
（Ⅰ）求证：平面EAC⊥平面PBC；
（Ⅱ）求二面角P-AC-E的余弦值；
（Ⅲ）求直线PA与平面EAC所成角的正弦值．
，动点
在圆
上运动，以
，
为两边作平行四边形
，求点
的轨迹．
上，且到
轴的距离恰等于圆的半径，在
轴上截得的弦长为
，求此圆的方程．
的底边长分别为6和4，高为3，求这个等腰梯形的外接圆的方程，并求这个圆的圆心坐标和半径长．
内一点
，过点
的直线
的倾斜角为
，直线
，
．（1）当
时，求
的长；（2）当弦
被圆
截得的弦
的长．相关知识点
推荐套卷
（本小题满分14分）如图，在四棱锥P-ABCD中，四边形ABCD是直角梯形，AB⊥AD，AB∥CD，PC⊥底面ABCD，PC=AB=2AD=2CD=2，E是PB的中点．
（Ⅰ）求证：平面EAC⊥平面PBC；
（Ⅱ）求二面角P-AC-E的余弦值；
（Ⅲ）求直线PA与平面EAC所成角的正弦值．
粤公网安备 44130202000953号