（本小题满分14分）设数列{an}满足：a1=1，an+1=3an，n∈N*．设Sn为数列{bn}的前n项和，已知b1≠0，2bn–b1=S1•Sn，n∈N*．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）设cn=bn•log3an，求数列{cn}的前n项和Tn；
（Ⅲ）证明：对任意n∈N*且n≥2，有
+
++
＜
．
相关试题
＋loga
＋…＋loga
＝logam＋logan，求m、n的值．
的值．
＋
＝
；
－lg
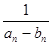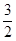＋lg12.5－log89·log278；推荐套卷
（本小题满分14分）设数列{an}满足：a1=1，an+1=3an，n∈N*．设Sn为数列{bn}的前n项和，已知b1≠0，2bn–b1=S1•Sn，n∈N*．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）设cn=bn•log3an，求数列{cn}的前n项和Tn；
（Ⅲ）证明：对任意n∈N*且n≥2，有+++＜．
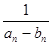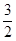粤公网安备 44130202000953号