如图所示,四棱锥
的底面
是半径为
的圆的内接四边形,其中
是圆的直径,
,
,
垂直底面
,
分别是
上的点,且
,过点
作
的平行线交
于
.
(1)求
与平面
所成角
的正弦值
(2)证明:
是直角三角形;
(3)当
时,求
的面积.
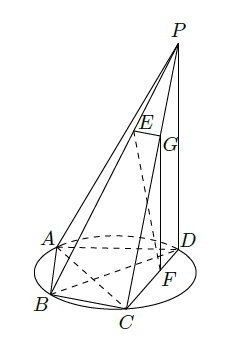
推荐套卷
如图所示,四棱锥
的底面
是半径为
的圆的内接四边形,其中
是圆的直径,
,
,
垂直底面
,
分别是
上的点,且
,过点
作
的平行线交
于
.
(1)求
与平面
所成角
的正弦值
(2)证明:
是直角三角形;
(3)当
时,求
的面积.
