（本小题满分13分）将编号为1，2，3，4的4个小球随机放到A、B、C三个不同的小盒中，每个小盒至少放一个小球．
（Ⅰ）求编号为1， 2的小球同时放到A盒的概率；
（Ⅱ）设随机变量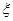
为放入A盒的小球的个数，求的分布列与数学期望．
相关试题
（
为实数，
，
）．
的图像过点
，且方程
有且只有一个根，求
当
，
，
，且函数
能否大于
？
的定义域
满分12分）已知
是椭圆
的两个焦点，
是椭圆上的点，且
．
的周长；相关知识点
推荐套卷
（本小题满分13分）将编号为1，2，3，4的4个小球随机放到A、B、C三个不同的小盒中，每个小盒至少放一个小球．
（Ⅰ）求编号为1， 2的小球同时放到A盒的概率；
（Ⅱ）设随机变量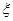为放入A盒的小球的个数，求的分布列与数学期望．
粤公网安备 44130202000953号