(12分)某地电话拨号入网有两种收费方式，用户可以任选其一：
方法一：计时制：0．05元/分；
方法二：包月制：50元/月（限一部个人住宅电话上网）．
此外，每一种上网方式都得加收通信费0．02元/分．
（1）设某用户某月上网的时间为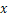
小时，请你分别写出两种收费方式下该用户应该支付的费用；
（2）若某用户估计一个月内上网的时间为20小时，你认为采用哪种方式较为合算？
相关试题
(12分)某地电话拨号入网有两种收费方式，用户可以任选其一：
方法一：计时制：0．05元/分；
方法二：包月制：50元/月（限一部个人住宅电话上网）．
此外，每一种上网方式都得加收通信费0．02元/分．
（1）设某用户某月上网的时间为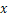小时，请你分别写出两种收费方式下该用户应该支付的费用；
（2）若某用户估计一个月内上网的时间为20小时，你认为采用哪种方式较为合算？
，然后再选一个你喜欢的数代入求值．
和
中，
，
，
，且点
在一条直线上，连接
分别为
的中点．
；
是等腰三角形；
（3）在图①的基础上，将
按顺时针方向旋转，使D点落在线段AB上，其他条件不变，得到图②所示的图形．（1）、（2）中的两个结论是否仍然成立吗？请你直接写出你的结论．
粤公网安备 44130202000953号