（本小题满分16分）设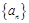
是公差为
的等差数列，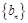
是公比为
(
)的等比数列．记
．
（1）求证：数列
为等比数列；
（2）已知数列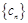
的前4项分别为4，10，19，34．
① 求数列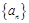和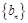的通项公式；
② 是否存在元素均为正整数的集合
，
，…，
(
，
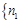)，使得数列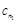
，
，…，
为等差数列？证明你的结论．
相关试题
是公比为q的等比数列. 
不是等比数列.
的前
项和为
，且
，
.
的前
，且
(
为常数)，令
，求数列
的前
。
的前
项和为
.已知
,
,
.
的值；
.
的前n项和为
.已知
，且
成等比数列，求
，其前
项和
满足
且
是
和
的等比中项..
的通项公式；
，求数列
的前99项和.推荐套卷
（本小题满分16分）设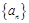是公差为的等差数列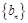，是公比为()的等比数列．记．
（1）求证：数列为等比数列；
（2）已知数列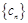的前4项分别为4，10，19，34．
① 求数列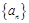和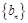的通项公式；
② 是否存在元素均为正整数的集合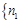，，…，(，)，使得数列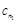，，…，为等差数列？证明你的结论．
粤公网安备 44130202000953号