(本小题满分12分)2014年APEC峰会于11月10-11日在北京召开.据志愿服务联合会的统计显示:APEC领导人会议周期间,2000名志愿者共上岗服务11219人次,累计服务132022小时,所有的志愿者来自全国四大地理区域,数据如下表所示:
地理区域
|
北方地区
|
南方地区
|
西北地区
|
青藏地区
|
志愿者人数
|
600
|
800
|
400
|
200
|
为了更进一步了解有关信息,采用分层抽样的方法从上述四大地理区域的志愿者中随机抽取50名参加问卷调查.
(Ⅰ)从参加问卷调查的50名志愿者中随机抽取两名,求这两名来自同一地理区域的概率;
(Ⅱ)在参加问卷调查的50名志愿者中,从来自北方地区、西北地区的志愿者中随机抽取两名,用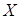 表示抽得北方地区志愿者的人数,求
表示抽得北方地区志愿者的人数,求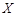 的分布列和数学期望.
的分布列和数学期望.