(本小题满分14分)已知向量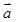 =(
=( ,1),向量
,1),向量 =(sin2x,cos2x),函数
=(sin2x,cos2x),函数
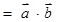
(1)求函数 的表达式,并作出函数
的表达式,并作出函数 在一个周期内的简图(用五点法列表描点);
在一个周期内的简图(用五点法列表描点);
(2)求函数 的周期,并写单调区间.
的周期,并写单调区间.
相关知识点
推荐套卷
(本小题满分14分)已知向量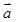 =(
=( ,1),向量
,1),向量 =(sin2x,cos2x),函数
=(sin2x,cos2x),函数
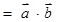
(1)求函数 的表达式,并作出函数
的表达式,并作出函数 在一个周期内的简图(用五点法列表描点);
在一个周期内的简图(用五点法列表描点);
(2)求函数 的周期,并写单调区间.
的周期,并写单调区间.