顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
(1)在网格中画出△ABC向上平移4个单位后得到的△A1B1C1;
(2)在网格中画出△ABC绕点A逆时针旋转90°后得到的△AB2C2;
(3)在(1)中△ABC向上平移过程中,求边AC所扫过区域的面积.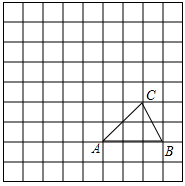
顶点在网格交点的多边形叫做格点多边形,如图,在一个9×9的正方形网格中有一个格点△ABC.设网格中小正方形的边长为1个单位长度.
(1)在网格中画出△ABC向上平移4个单位后得到的△A1B1C1;
(2)在网格中画出△ABC绕点A逆时针旋转90°后得到的△AB2C2;
(3)在(1)中△ABC向上平移过程中,求边AC所扫过区域的面积.