安庆迎江区农民张大伯为了致富奔小康,大力发展家庭养殖业,他准备用40米长的木栏围一个矩形的养圈,为了节约材料,同时要使矩形面积最大,他利用了自己家房屋一面长25米的墙,设计了如图一个矩形的养圈。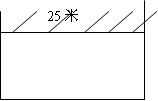
(1)请你求出张大伯设计的矩形养圈的面积。
(2)请你判断他的设计方案是否使矩形养圈的面积最大?如果不是最大,应怎样设计?请说明理由。
相关知识点
推荐套卷
安庆迎江区农民张大伯为了致富奔小康,大力发展家庭养殖业,他准备用40米长的木栏围一个矩形的养圈,为了节约材料,同时要使矩形面积最大,他利用了自己家房屋一面长25米的墙,设计了如图一个矩形的养圈。
(1)请你求出张大伯设计的矩形养圈的面积。
(2)请你判断他的设计方案是否使矩形养圈的面积最大?如果不是最大,应怎样设计?请说明理由。