(本大题15分)已知直角坐标系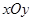 中,以
中,以 为中心,点
为中心,点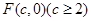 为焦点的椭圆
为焦点的椭圆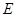 经过第一象限的点
经过第一象限的点 ,
,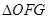 的面积为
的面积为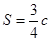 ,且
,且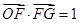 .
.
(1)当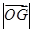 取最小值时,求椭圆
取最小值时,求椭圆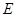 的标准方程;
的标准方程;
(2)在(1)的条件下,设点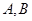 分别为椭圆
分别为椭圆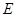 的左、右顶点,点
的左、右顶点,点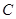 是椭圆的下顶点,点
是椭圆的下顶点,点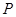 在椭圆
在椭圆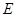 上(与点
上(与点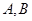 均不重合),点
均不重合),点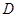 在直线
在直线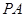 上,若直线
上,若直线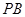 的方程为
的方程为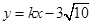 ,且
,且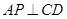 ,试求直线
,试求直线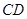 的方程.
的方程.
推荐套卷
(本大题15分)已知直角坐标系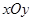 中,以
中,以 为中心,点
为中心,点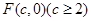 为焦点的椭圆
为焦点的椭圆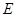 经过第一象限的点
经过第一象限的点 ,
,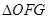 的面积为
的面积为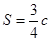 ,且
,且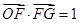 .
.
(1)当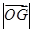 取最小值时,求椭圆
取最小值时,求椭圆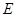 的标准方程;
的标准方程;
(2)在(1)的条件下,设点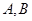 分别为椭圆
分别为椭圆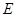 的左、右顶点,点
的左、右顶点,点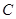 是椭圆的下顶点,点
是椭圆的下顶点,点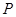 在椭圆
在椭圆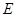 上(与点
上(与点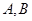 均不重合),点
均不重合),点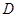 在直线
在直线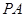 上,若直线
上,若直线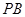 的方程为
的方程为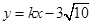 ,且
,且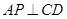 ,试求直线
,试求直线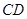 的方程.
的方程.