(本小题满分14分)
如图,直线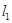 和
和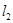 相交于点
相交于点 且
且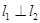 ,点
,点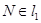 .以
.以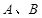 为端点的曲线段C上的任一点到
为端点的曲线段C上的任一点到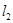 的距离与到点
的距离与到点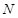 的距离相等.若
的距离相等.若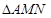 为锐角三角形,
为锐角三角形,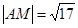 ,
,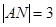 ,且
,且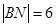 .
.
(1)曲线段C是哪类圆锥曲线的一部分?并建立适当的坐标系,求曲线段C所在的圆锥曲线的标准方程;
(2)在(1)所建的坐标系下,已知点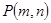 在曲线段C上,直线
在曲线段C上,直线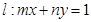 ,求直线
,求直线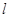 被圆
被圆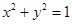 截得的弦长的取值范围.
截得的弦长的取值范围.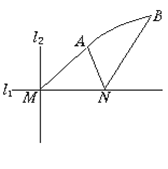
推荐套卷
(本小题满分14分)
如图,直线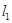 和
和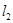 相交于点
相交于点 且
且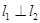 ,点
,点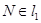 .以
.以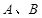 为端点的曲线段C上的任一点到
为端点的曲线段C上的任一点到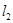 的距离与到点
的距离与到点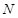 的距离相等.若
的距离相等.若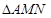 为锐角三角形,
为锐角三角形,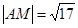 ,
,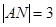 ,且
,且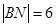 .
.
(1)曲线段C是哪类圆锥曲线的一部分?并建立适当的坐标系,求曲线段C所在的圆锥曲线的标准方程;
(2)在(1)所建的坐标系下,已知点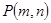 在曲线段C上,直线
在曲线段C上,直线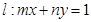 ,求直线
,求直线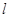 被圆
被圆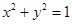 截得的弦长的取值范围.
截得的弦长的取值范围.