（本小题满分14分）下图是一块平行四边形园地ABCD，经测量，AB=20m，BC=10m，∠ABC=120°．拟过线段AB上一点E设计一条直路EF（点F在四边形ABCD的边上，不计路的宽度），将该园地分为面积之比为3:1的左、右两部分分别种植不同花卉．设EB=x，EF=y（单位：m）．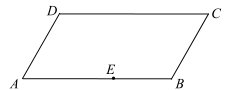
（Ⅰ）当点F与点C重合时，试确定点E的位置；
（Ⅱ）求y关于x的函数关系式；
（Ⅲ）请确定点E，F的位置，使直路EF长度最短．
相关试题
，
，求最小边的边长。
和
满足：
，数列
是等差数列，
为数列
项和，且
，
，使
？若存在，求出
，若不存在，说明理由。
，
，
平行的单位向量
；
，若存在
使得
成立，求
的取值范围。
中，
分别是角
的对边，
，求
的值.
.
的最小正周期和单调递增区间；
满足
，求角推荐套卷
（本小题满分14分）下图是一块平行四边形园地ABCD，经测量，AB=20m，BC=10m，∠ABC=120°．拟过线段AB上一点E设计一条直路EF（点F在四边形ABCD的边上，不计路的宽度），将该园地分为面积之比为3:1的左、右两部分分别种植不同花卉．设EB=x，EF=y（单位：m）．
（Ⅰ）当点F与点C重合时，试确定点E的位置；
（Ⅱ）求y关于x的函数关系式；
（Ⅲ）请确定点E，F的位置，使直路EF长度最短．
粤公网安备 44130202000953号