如图,△ABC中,∠C=Rt∠,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?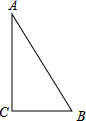
如图,△ABC中,∠C=Rt∠,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?