（本题满分14分 ，第（1）小题5分，第（2）小题5分，第（3）小题4分）
如图，已知在等腰 Rt△ABC中，∠C＝90°，斜边AB＝2，若将△ABC翻折，折痕EF分别交边AC、边BC于点E和点F（点E不与A点重合，点F不与B点重合），且点C落在AB边上，记作点D．过点D作DK⊥AB，交射线AC于点K，设AD＝x，y＝cot∠CFE，
（1）求证：△DEK∽△DFB；
（2）求y关于x的函数解析式并写出定义域；
（3）联结CD，当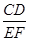
＝
时，求x的值
相关试题
如图，点E在△ABC外部，点D在BC边上，DE交AC于点F，若∠1＝∠2＝∠3，AC＝AE。试说明下列结论正确的理由：(1) ∠C=∠E； (2) AB=AD．
已知：如图，O为坐标原点，四边形OABC为矩形，A(10，0)，C(0，4)，点D是OA的中点，点P在BC上以每秒1个单位的速度由C向B运动。
(1) 求梯形ODPC的面积S与时间t的函数关系式。
(2) t为何值时，四边形PODB是平行四边形？
(3) 在线段PB上是否存在一点Q，使得ODQP为菱形。若存在求t值，若不存在，说明理由。
(4) 当△OPD为等腰三角形时，求点P的坐标。
相关知识点
推荐套卷
粤公网安备 44130202000953号