为响应环保组织提出的“低碳生活”的号召,李明决定不开汽车而改骑自行车上班.有一天,李明骑自行车从家里到工厂上班,途中因自行车发生故障,修车耽误了一段时间,车修好后继续骑行,直至到达工厂(假设在骑自行车过程中匀速行驶).李明离家的距离y(米)与离家时间x(分钟)的关系表示如下图: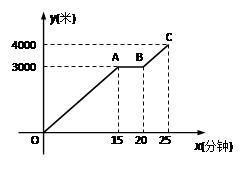
李明从家出发到出现故障时的速度为 米/分钟;
李明修车用时 分钟;
求线段BC所对应的函数关系式(不要求写出自变量的取值范围).
相关知识点
推荐套卷
 。
。 。
。 。
。

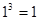 ,
,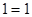 ,
, ,
, ,
,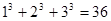 ,
,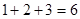 ,
,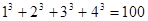 ,
, ,
, 等于什么?
等于什么? 等于什么?
等于什么?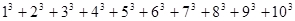 的值.
的值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号