（本题本题10分）如图，在平面直角坐标系中，O是坐标原点，抛物线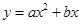
与
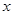轴正半轴交于点A，对称轴DE交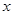轴于点E．点B在第二象限，过点B作BC⊥x轴于点C，连结AB，且AB=10，AC=8．将点B向右平移5个单位后，恰好与抛物线的顶点D重合．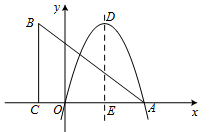
（1）求点D的坐标；
（2）求该抛物线的解析式．
，求这个多边形的边数．
相关知识点
推荐套卷
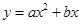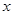（本题本题10分）如图，在平面直角坐标系中，O是坐标原点，抛物线与轴正半轴交于点A，对称轴DE交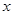轴于点E．点B在第二象限，过点B作BC⊥x轴于点C，连结AB，且AB=10，AC=8．将点B向右平移5个单位后，恰好与抛物线的顶点D重合．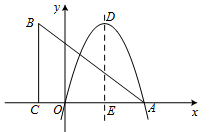
（1）求点D的坐标；
（2）求该抛物线的解析式．
粤公网安备 44130202000953号