2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:

(Ⅰ)根据频率分布直方图,求a的值,并估计众数,说明此众数的实际意义;
(Ⅱ)从“能接受的最高票价”落在 [8,10),[10,12]的被调查者中各随机选取3人进行追踪调查,记选中的6人中35岁以上(含35岁)的人数为X,求随机变量X的分布列及数学期望.
相关知识点
推荐套卷
 分别是椭圆
分别是椭圆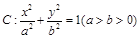 的左、右顶点,点
的左、右顶点,点 在椭圆
在椭圆 上,且直线
上,且直线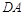 与直线
与直线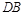 的斜率之积为
的斜率之积为 .
.
 是椭圆
是椭圆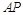 与
与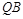 交于点
交于点 ,直线
,直线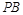 与
与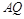 交于点
交于点 .若弦
.若弦 过椭圆的右焦点
过椭圆的右焦点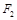 ,求直线
,求直线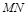 的方程.
的方程. 的底面是直角梯形,
的底面是直角梯形,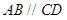 ,
, ,
, 和
和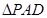
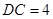 ,
, 为
为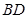 的中点,
的中点,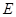 为
为 的中点.
的中点.
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.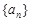 是各项均不为零的等差数列,公差为
是各项均不为零的等差数列,公差为 ,
, 为其前
为其前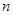 项和,且满足
项和,且满足 ,
, .数列
.数列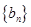 满足
满足 ,
,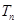 为数列
为数列 和
和 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有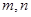 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.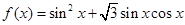 ,
,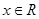
 的最小正周期,并求
的最小正周期,并求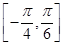 上的最小值;
上的最小值;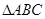 中,
中,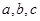 分别是角
分别是角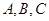 的对边,
的对边,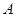 为锐角,若
为锐角,若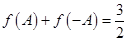 ,
,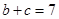 ,
, ,求
,求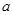 .
. ,若
,若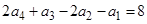 ,则
,则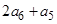 的最小值为 .
的最小值为 . 粤公网安备 44130202000953号
粤公网安备 44130202000953号